Continuous Uniform Distribution

Continuous Uniform Distribution#

Definition#

Definition 115 (Continuous Uniform Distribution (PDF))

\(X\) is a continuous random variable with a continuous uniform distribution if the probability density function is given by:

(187)#\[\begin{split} \pdf(x) = \begin{cases} \frac{1}{b-a} & \text{if } a \leq x \leq b \\ 0 & \text{otherwise} \end{cases} \end{split}\]

where \([a,b]\) is the interval on which \(X\) is defined.

Some conventions:

  1. We write \(X \sim \uniform(a,b)\) to indicate that \(X\) has a continuous uniform distribution on \([a,b]\).

Definition 116 (Continuous Uniform Distribution (CDF))

If \(X\) is a continuous random variable with a continuous uniform distribution on \([a,b]\), then the CDF is given by integrating the PDF defined in Definition 115:

(188)#\[\begin{split} \cdf(x) = \begin{cases} 0 & \text{if } x < a \\ \frac{x-a}{b-a} & \text{if } a \leq x \leq b \\ 1 & \text{if } x > b \end{cases} \end{split}\]

The PDF and CDF of two continuous uniform distributions are shown below.

Hide code cell source

 
 1import warnings
 2
 3warnings.filterwarnings("ignore")
 4import numpy as np
 5import matplotlib.pyplot as plt
 6
 7from scipy import stats
 8
 9fig, axes = plt.subplots(2, 2, figsize=(10, 10))
10
11u = np.linspace(-1, 9, 5000) # random variable realizations
12U1 = stats.uniform(0.2, 0.8)
13
14axes[0, 0].plot(u, U1.pdf(u), "r-", lw=3, alpha=0.6, label="Uniform[0.2, 0.8]")
15axes[0, 0].set_title("PDF of Uniform[0.2, 0.8]")
16axes[0, 0].set_xlim(-0.1, 1.3)
17axes[0, 0].set_ylim(0, 3)
18axes[0, 0].set_xlabel("x")
19axes[0, 0].set_ylabel("pdf(x)")
20
21axes[0, 1].plot(u, U1.cdf(u), "r-", lw=3, alpha=0.6, label="Uniform[0.2, 0.8]")
22axes[0, 1].set_title("CDF of Uniform[0.2, 0.8]")
23axes[0, 1].set_xlim(-1, 10)
24axes[0, 1].set_ylim(0, 1.1)
25axes[0, 1].set_xlabel("x")
26axes[0, 1].set_ylabel("cdf(x)")
27
28U2 = stats.uniform(2, 6)
29
30axes[1, 0].plot(u, U2.pdf(u), "r-", lw=3, alpha=0.6, label="Uniform[2, 8]")
31axes[1, 0].set_title("PDF of Uniform[2, 8]")
32axes[1, 0].set_xlim(1, 9)
33axes[1, 0].set_ylim(0, 1.1)
34axes[1, 0].set_xlabel("x")
35axes[1, 0].set_ylabel("pdf(x)")
36
37axes[1, 1].plot(u, U2.cdf(u), "r-", lw=3, alpha=0.6, label="Uniform[2, 8]")
38axes[1, 1].set_title("CDF of Uniform[2, 8]")
39axes[1, 1].set_xlim(1, 9)
40axes[1, 1].set_ylim(0, 1.1)
41axes[1, 1].set_xlabel("x")
42axes[1, 1].set_ylabel("cdf(x)")
43
44
45plt.show()
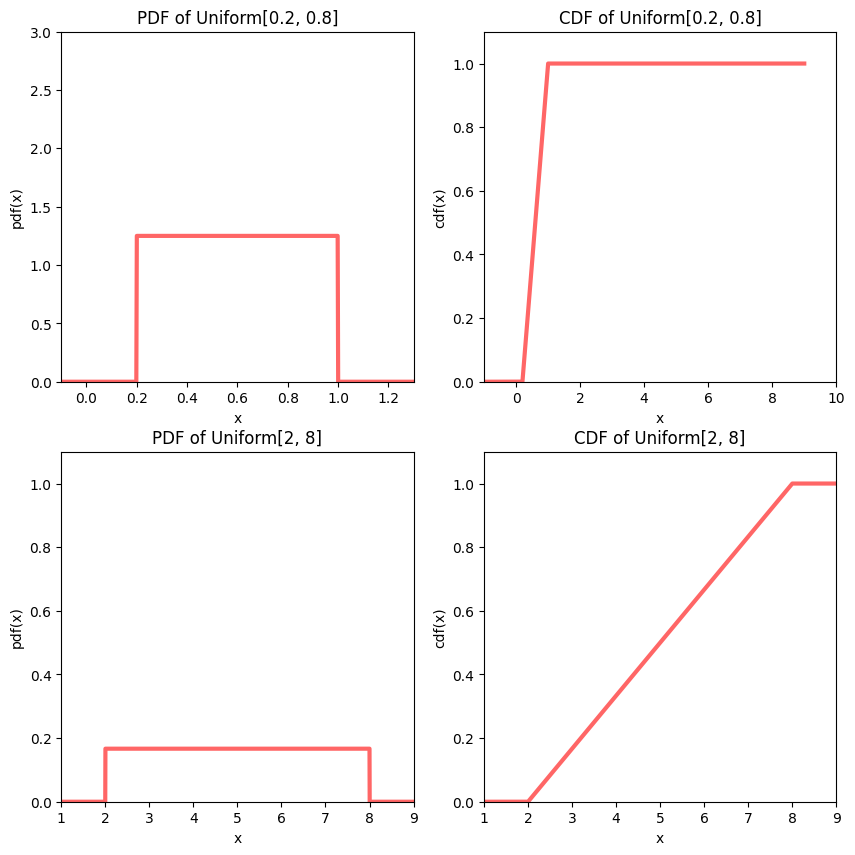
../../_images/413f7b88328a3089ec87c74b390006788642f3e41dc02c7b03762d3cc7bb53b5.png

Hide code cell source

 
 1import sys
 2from pathlib import Path
 3parent_dir = str(Path().resolve().parents[2])
 4sys.path.append(parent_dir)
 5
 6import numpy as np
 7import scipy.stats as stats
 8
 9from omnivault.utils.reproducibility.seed import seed_all
10from omnivault.utils.probability_theory.plot import plot_continuous_pdf_and_cdf
11seed_all()
12
13# x = np.linspace(-1, 9, 5000) # random variable realizations
14U1 = stats.uniform(0.2, 0.8)
15U2 = stats.uniform(2, 6)
16
17plot_continuous_pdf_and_cdf(U1, -1, 9, title="Uniform$([0.2, 0.8])$", xlim=(-0.1, 1.3), ylim=(0, 2))
18plot_continuous_pdf_and_cdf(U2, -1, 10, title="Uniform$([2, 6])$", xlim=(-1, 10), ylim=(0, 1.1))
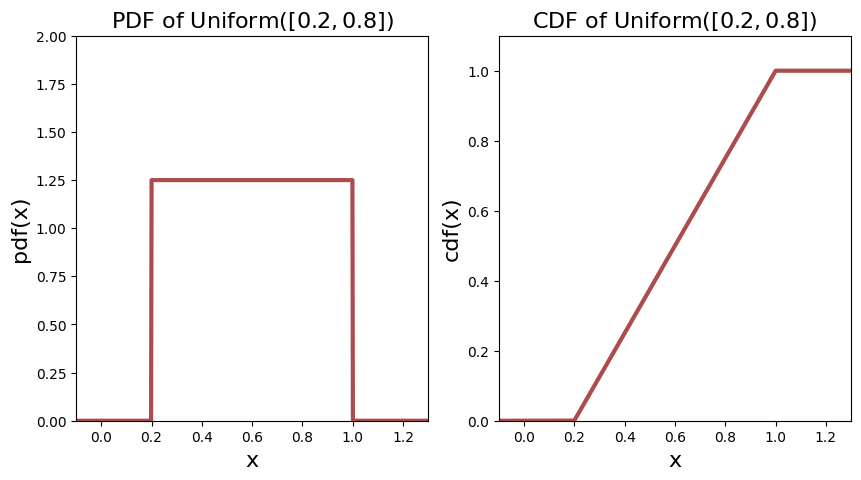
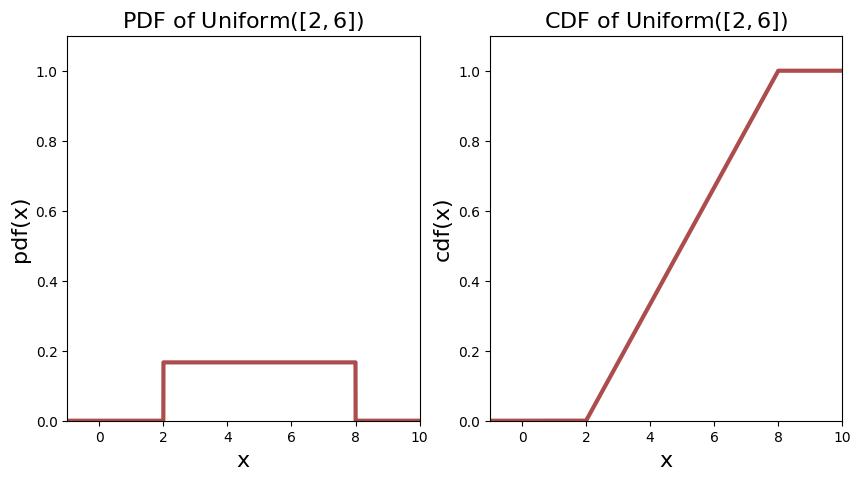
../../_images/e59c4e55d67c5421a08a9075a04b5cf5b3ecf34db087f15f1bc7d6feff54e5d5.png ../../_images/330373ee131f29ddf430340f9196070112f62dd60b0eff0d1c175abfb82b8290.png

Expectation and Variance#

Theorem 28 (Expectation and Variance of Continuous Uniform Distribution)

If \(X\) is a continuous random variable with a continuous uniform distribution on \([a,b]\), then

(189)#\[ \expectation \lsq X \rsq = \frac{a+b}{2} \qquad \text{and} \qquad \var \lsq X \rsq = \frac{(b-a)^2}{12} \]

Remark 45 (Intuition for Expectation and Variance of Continuous Uniform Distribution)

The expectation of a continuous uniform distribution is the midpoint of the interval on which the random variable is defined.

This should not be surprising, since the probability density function is constant over the interval, and the probability of any point in the interval is the same.

Let’s say we have \(X \sim \text{Uniform}(0, 10)\), then \(\expectation \lsq X \rsq = 5\).

References and Further Readings#

  • Chan, Stanley H. “Chapter 4.5. Uniform and Exponential Random Variables.” In Introduction to Probability for Data Science, 201-205. Ann Arbor, Michigan: Michigan Publishing Services, 2021.

  • Pishro-Nik, Hossein. “Chapter 4.2.1. Uniform Distribution” In Introduction to Probability, Statistics, and Random Processes, 248-248. Kappa Research, 2014.

Contents